The First Shall Be Last

Arthur Burks | published Jan, 1939

added Jun 6, 2024
cover Image
Download File ⭛
First Date of Publication
Jan, 1939
Original Source
Astounding Science Fiction
Medium
Short Story
Original Language
English
Kasman Review
Not in Kasman Database
ISFDB
Tags
Summary: A deft use of geodesics and energy equations to show that sometimes, the fastest path is not the shortest one.

Story Tag Line: Those lines—some five billions of miles long—would be weak as a baby’s breath. M times m over d squared—and d bein’ damn near infinity, so far as those little m’s go. But Uranus-Sun, now—with the Sun’s allmighty M multiplyin’ on top of the formula—aye, we’ve got a cable to haul on there. Then if we shunt off on the Earth-Venus lines—and cut across close round Earth to the Mars-Earth lines, we’ll pick up the heaviest lines in all the System—the Jupiter-Sun lines—to haul us out again !”

Back Images:
Back Image
Back Image

Reviews

  • Vijay Fafat
    Published on

    A fairly decently written story about a slow space-freighter which outguns a modern spaceship in a cosmic race by using some geometry of geodesics – that the fastest way to travel between two points in space is not along the straight line connecting them but along a gravity-optimized geodesic, which may look very complicated relative to a straight line but which will get the job of minimizing travel time, if done efficiently. Along the way, there is also some biting, sarcastic commentary on how the fruits of success can be sour – you can be too successful for your own good – and how hierarchy always usurps credit for success.

    “Arachne” is a space freighter which has just delivered a cargo to Uranus when it gets orders to head to Pluto to pick up a consignment of Element 103. Complicating matters is the fact that a rival transport company has sent its own, modern spaceship, “Comet”, from Earth straight toward Pluto for the same consignment, at a time when Earth-Pluto distance is smaller than Uranus-Pluto. The first to Pluto wins. From there, it is a battle of wits and celestial geometry and the use of slingshot manoeuvres for Arachne to beat the faster spaceship…

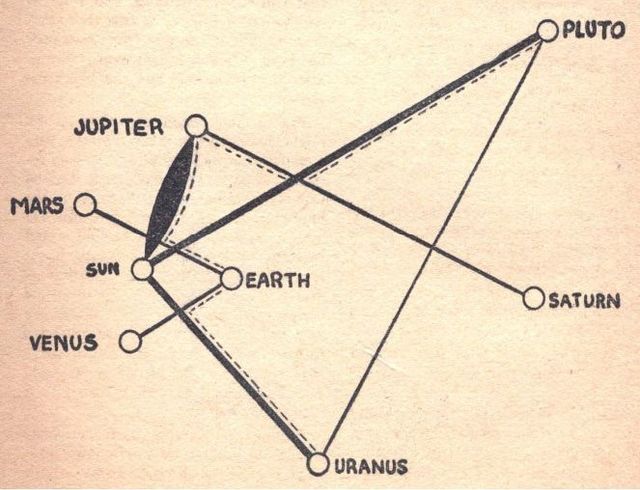
    The author shows a geometrical map of the relative locations of the various planets and the sun to aid a partial visualization of the problem.

    The mathematical content is not laid out in so many words as built into the narrative between Arachne’s chief engineer and its captain.